A matrix can be entered into the worksheet in a very simple way.
Using the "New matrix" button
When you click on the 
(New matrix) button, you will be prompted to select the number of columns and rows of the matrix that you want to enter. Once you select this, you will see a template that looks like this:
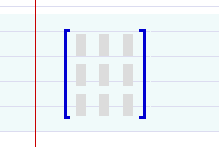
You can fill in the entries by using either the mouse or the "TAB" key.
In order to make the cursor exit the matrix, press the 
key.
Operations with matrices
You can add (or subtract) matrices of the same size by using the "+" (or "-") signs.
You can also multiply a matrix by a scalar and multiply two matrices together. In order to perform a matrix multiplication operation, you need to make certain that the number of COLUMNS of the FIRST MATRIX is equal to the number of ROWS of the SECOND MATRIX.
Finding the inverse of a matrix
In order to tell Algebrator that you wish to calculate the inverse of a certain matrix, you simply add the "-1" exponent to the matrix. This can be accomplished in two different ways:
First way:
- Press the
button. - Enter the matrix whose inverse you want to find.
- Fill all the entries of the matrix with the desired values.
- Press the key to make the cursor "leave" the matrix.
- Press "^" - the cursor will be blinking "up" in the exponent area.
- Type the "-1" exponent.
Second way:
- Press the button.
- Press the
(new power) button - this will create a "power" template. - Press the (new matrix) button.
- Fill all the entries of the matrix with the desired values.
- Press the key to make the cursor exit the matrix.
- Press the
key to make the cursor go "up" to the exponent area. - Type the "-1" exponent.
Should I verify if the matrix is invertible before trying to find its inverse?
No, that is not necessary. If you enter a non-invertible matrix, Algebrator will inform you and will ask you if you wish to find its determinant (so that you can see that it is equal to zero, which is the indicator that the matrix is not invertible).
Watch Video
Related help topics